Il y a un principe mathématique simple caché derrière la longueur des tubes d’une flûte de pan, et de tous les instruments qui font intervenir une « longueur vibrante » (piano, instruments à cordes…). C’est le nombre « racine douzième de deux ». Voyons cela de plus près… (je vous conseille de prendre un crayon et une feuille… mais vous allez voir, ça va bien se passer !)
Sur tous ces instruments, si une longueur l (de corde, de tube, etc…) produit la note n, la longueur l/2 produira la même note n à l’octave supérieure. Exemple : si une corde de guitare de 1 m de long donne un mi, la même corde de guitare de 50 cm, avec la même tension, donnera un mi à l’octave supérieure. Si vous jouez de la guitare, vérifiez-le : faites sonner le mi grave. Puis mesurez la position du milieu exact de la corde (vous constaterez que ce point coïncide avec la position de la frette supérieure de la douzième case). Posez votre doigt sur cette case (ce qui a l’effet de raccourcir la corde à sa demi longueur) et faites sonner la corde : elle produit un mi à l’octave supérieure ! La même corde de guitare, de 2 mètres de long, donnerait (si elle existait) un mi à l’octave inférieure.
La flûte de pan n’échappe pas à ce principe. Si vous avez une flûte entre les mains, vérifiez par vous même : prenez le tube le plus long et mesurez-le. Cherchez le tube de votre flûte de pan qui mesure exactement la moitié de cette longueur et soufflez dedans : il produit la même note, à l’octave supérieure.
Partant de cette constatation universelle, on peut tirer une règle mathématique simple permettant de calculer la longueur des tubes d’une flûte de pan, d’une octave à l’autre. Pour cela : partir du tuyau le plus grave, et diviser sa longueur par 2, on obtient l’octave suivante. Recommencer sur autant d’octaves que souhaité. Cette règle mathématique s’appelle une « progression géométrique de raison 1/2 » (ou 0,5, ce qui est la même chose).
Ya pas, on est plus savants comme ça.
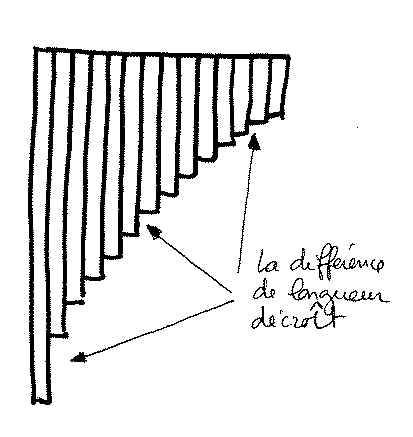
Sur 4 octaves, les tubes d’une flûte de pan produisant la note de même nom mesureraient par exemple : 40 cm, 20 cm, 10 cm, 5 cm. On remarque que, comme toute progression géométrique, le dessin tracé par les extrémités inférieures des tubes de la flûte ne forme pas une droite, mais une courbe dont la pente diminue lorsque l’on se dirige vers les aigus, qui s’appelle une parabole dans le langage mathématique.
A partir de cette règle de l’octave, comment améliorer le principe de calcul pour nous permette de calculer non seulement les longueurs des tubes d’octave, mais aussi la longueur des 11 tubes intermédiaires (car nos gammes occidentales comptent 12 degrés, voir l’encadré ci-dessous) ?
Pourquoi 12 degrés dans une octave ?
Dans nos sociétés occidentales, on a pris l’habitude de diviser une octave en 12 intervalles. C’est comme ça, on y est habitués, tout autre découpage sonne « bizarre » à nos oreilles formatées par des siècles d’écoute. Ces intervalles sont appelés des « demi-tons ». On les retrouve sur tous les instruments. Jetez un coup d’œil à un piano : d’un do à l’autre il y a 7 touches blanches, et 5 touches noires, ça fait 12. Sur une guitare, il y a 12 cases pour arriver à l’octave à mi longueur du manche…
Pourtant, dans une octave de flûte de pan, sauf cas particuliers rares (mais sans doute de plus en plus fréquent dans l’avenir) il n’y a généralement que 7 tubes. Pourquoi ? Parce que la plupart des flûtes de pan actuelles sont « diatoniques ». Pour jouer des airs d’origine traditionnelle, il n’y a souvent pas besoin des touches noires du piano, on peut se contenter des touches blanches. La flûte de pan n’a donc « que des touches blanches ». Mais on pourrait (et ça commence à se faire) rajouter les 5 touches noires entre les touches blanches aux endroits adéquats…
Supposons qu’il existe une loi mathématique permettant de trouver successivement la longueur de tous les tubes suivantes à partir de la longueur d’un premier tube. Ce serait une progression géométrique, de même nature que celle qu’on vient de voir pour le calcul des octaves, mais de « raison » différente. Essayons de calculer cette raison. Appelons-la r.
Ce nombre r devra présenter les deux propriétés suivantes :
- Lorsqu’on multiplie la longueur d’un tube par r, cela nous donne la longueur du tube suivant
- Lorsque l’on répète 12 fois la manœuvre, la longueur du 13ème tube (c’est à dire le premier tube de l’octave suivante) est égale à la moitié de la longueur du 1er tube.
Posons tout cela en termes mathématiques : si l1 est la longueur du premier tube, l2 la longueur du second tube… l13 la longueur du 13ème tube, r doit être tel que :
(1) l1 . r = l2, l2 . r = l3 … et enfin l12 . r = l13
et
(2) l13 = l1 / 2
Dans la suite d’expressions (1), remplaçons à chaque fois les différentes valeurs de r par leur développement : si l1 . r = l2 et l2 . r = l3, alors l1 . r . r = l3. Oui, mais comme l3 . r = l4, alors l1 . r . r . r = l4. On répète le procédé 12 fois de suites jusqu’à l13 et on arrive à :
l1 . r . r . r . r . r . r . r . r . r . r . r . r = l13 ce qui donne
l1 . r12= l13 ou
r12 = l13 / l1 et avec (2)
r12 = l1 / (l1 * 2) l1 s’élimine, il reste
r12 = 1/2
r = 1 / V122
En français : r est l’inverse de la racine douzième de 2. Ce nombre vaut 0,94387431. Il sert à calculer les longueurs successives de tubes de longueurs décroissantes, c’est à dire en partant du plus grand pour aller vers le plus petit.
Pour calculer les longueurs de tubes dans l’autre sens, on utilise V122, la racine douzième de 2. C’est le nombre magique de calcul des longueurs vibrantes en musique !
Grâce à ce nombre, il vous suffit donc de connaître la longueur d’un seul tube (ou de la longueur à vide de la guitare) pour calculer la longueur de tous les autres tubes (ou la position des frettes successives de la guitare…)